Jacob is similar. It is derived from an old Hebrew names and there are a ton of variants (including James and Diego)

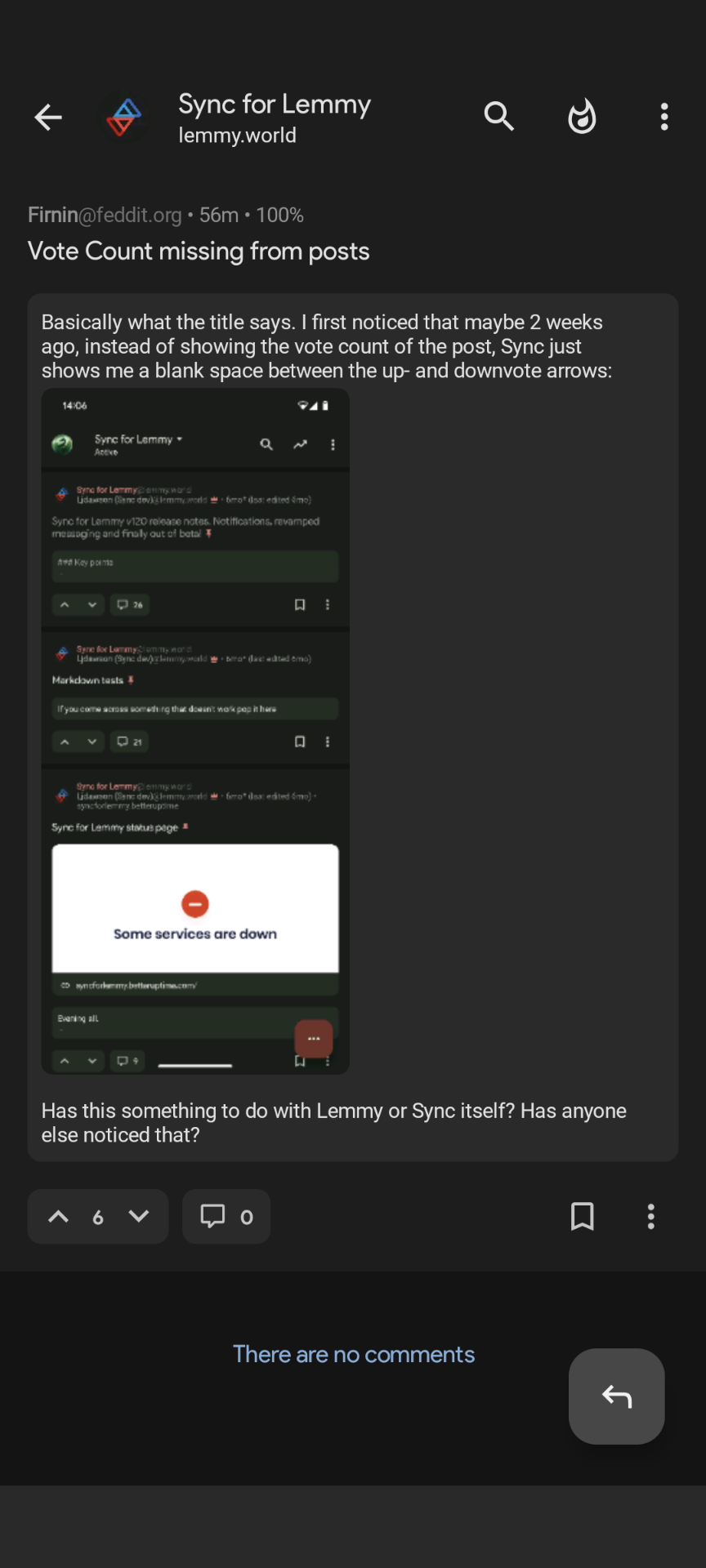
Roberto Bolaño. 2666 and The Savage Detectives are great. He also wrote a ton of short stories. His writing is also pretty straightforward so it’s easy to follow if you’re still learning.

Luis Sepúlveda. The Old Man who Read Love Stories and The Story of a Seagull and the Cat Who Taught Her To Fly are both very good. The latter is more of a children’s book but still worth it.

This page contains a collection of many authors and short stories. I’ve found it helpful: Literatura.us

This is another great resource for popular books by country: https://preply.com/en/d/most-translated-books–lp

Also, don’t they need to run to move food through their digestive tract? Or to force themselves to cough if they have something stuck in their lungs? I think there is some sort of dependency of basic functions that relies on the movement of their lungs/stomach going back and forth while running that they can’t easily do if they just stand in one place all day

deleted by creator

“Enabling shareholders to profit was seen as a means to that end.”

Right, that’s the part I take issue with. Why is there a profit on a public good?

I agree with all of the restrictions in place, but those have gotten weaker over time, when they should’ve gotten more restrictive. The problem with allowing them to profit is that over time, the profit gives them more bargaining power which allows them to erode the oversight and avoid all consequences for breaking the regulations.

I get your point, but I have trouble understanding how acting in the public interest and charging over operating costs can be compatible, especially in public service areas like hospitals/medicine and education.

“Is there any reason why this needs to be a taxpayer subsidized organization?”

Public safety? Is that a good enough reason? We should be subsiding more things that are in the public interest - programs that benefit the public should never be run by for-profit corporations.

Have you thought of trying to pick up another language? Started learning Spanish 4 years ago and now I can go on vacation and have conversations with locals. Also, I’m more interested in their local history because I can read it/listen to it in Spanish and practice the language at the same time.

I see vote counts. Is it possible that your instance blocks them for some reason?

I mean, it’s pretty well documented how awful Christopher Columbus was. Even in the context of the time period: he was arrested in the new world and shipped back to Spain for a trial because he was so ruthless in his treatment of the native peoples. The myths about him being a ‘great man’ are all only like 100 years old.

Oh my God, I read that as “Kissinger” and thought for a terrible moment that he was still alive.

Also possible that there may have been multiple in the household if so many were printed and mailed out? Maybe they turned the real one in for the prize money and then kept a non-winning one in a scrap book? Memories over time are weird so they could’ve convinced themselves that they kept the real one

Thank you! I should’ve linked to it. The actual text does a much better job of answering OP than my attempt to summarize it.

Especially in the US, where both parties are globally “right” in both political and financial aspects, a lot of time claiming to be a centrist means that you like capitalism and bombing other countries but you support LGBT causes and are pro-choice. I think, online and especially on lemmy, that the vocal left-wing voices (correctly) see this still as aiding the right but being too cowardly to admit it.

This also ties back to the MLK quote about the ‘white centrist’ being the biggest obstacle to his movement, because they may say the right things and appear to be helpful but take no action for the movement. By staying centrist and trying to meet in the middle, would lend credibility to the voices on the other side.

Either him or Seinfeld? Feels like the stand-up bit at the beginning of one of the early episodes.

The original draft probably said “nearly a 300% increase” and then the editor didn’t know the difference between percent increase and basic multiplication.

Right, isn’t that the point of the question? What old time things did we do for one reason (cloven hooves) that turned out to be right for completely different reasons (health and safety)

Three games

In the original the possibilities for a prize behind the doors 1,2,3 are:

A) YNN B) NYN C) NNY

In (A) - A.1 you choose door 1 and then stay, you win A.2 you choose door 1 and switch, you lose A.3 you choose door 2 and stay, you lose A.4 You choose door 2 and switch, you win A.5 you choose door 3 and stay, you lose A.6 you choose door 3 and switch, you win

By staying, you lose in 2 of 3 cases (A.3 and A.5)

By switching you only lose in 1 case (A.2)

It works out for (B) and © the same way. You have a 2/3rds chance of winning if you switch and a 1/3rd chance of winning if you don’t.

This isn’t a trick or anything, the math is pretty clear and you can actually write out all the scenarios and count it up yourself. It’s just a little counterintuitive because we aren’t used to thinking in terms of conditional probabilities this way.

Another way to think about it is the probability of losing. If the contestant loses, it means that they picked correctly on their first choice and then swapped. This will happen 1/3rd of the games, because there is a 1 in 3 chance of picking correctly the first time. So, if you have a 1/3rd chance of losing by swapping, then it follows that you have a 2/3rds chance of winning by swapping (choosing incorrectly at the start and then switching to the correct door)